Latitude and Longitude
Hopefully, this is something you learned in elementary school, but here’s a little refresher on latitude and longitude (which is the format in which we receive our boat’s location from our GPS module). Lines of latitude wrap around the Earth and give a position relative to the Equator (either north or south). Lines of longitude extend from the North Pole to the South Pole and give a position relative to the Prime Meridian (either east or west). Latitude and longitude are measured in degrees as shown in the figure below.
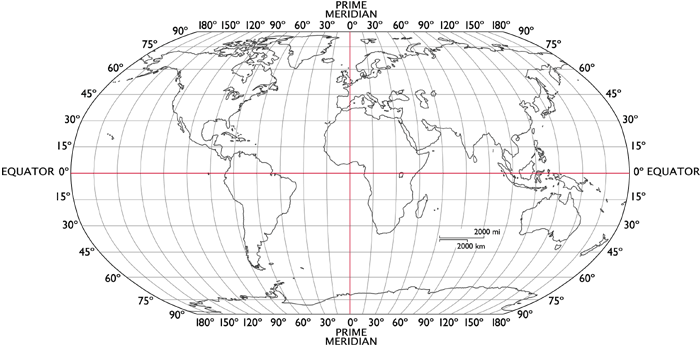
Latitude and longitude can either be expressed using decimal degrees or using degrees, minutes, and seconds. Decimal degrees are easily interpretable; for example, the decimal degree representation of Upson Hall’s location is latitude: 42.444241, longitude: -76.481933 (negative denotes south for latitude and west for longitude). Most GPS modules use this format. Considering the other format, a minute represents one sixtieth of a degree and a second represents one sixtieth of a minute. The cooresponding representation of Upson Hall’s location is 42°26’39.3”N 76°28’55.0”W (e.g. the latitude is 42 degrees, 26 minutes, and 39.3 seconds north of the Equator).
Notice that lines of latitude are equally spaced, while lines of longitude converge at the poles. The distance between lines of longitude is dependent on the latitude.
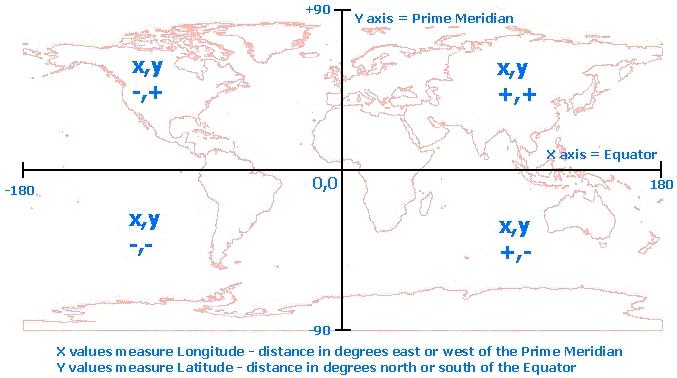
Approximated Cartesian
Because we are sailing within such a small area of the planet, we can safely ignore the curvature of the Earth and approximate our surroundings as a flat plane with units of meters. As shown below, the x-axis corresponds to the equator and the y-axis corresponds to the Prime Meridian.
Calculating the y-coordinate can be done with a simple conversion factor (where radEarth is the radius of the Earth):
\[y = radEarth * \pi /180 * latitude\]
Calculating the x-coordinate is slightly more complicated due to the convergence of lines of longitude at the poles:
\[x = radEarth * \pi /180 * \cos(latitude) * longitude\]
Due to being so far away from the global origin (the intersection of the Equator and the Prime Meridian), using this system can result in some really big numbers, which we can avoid by shifting our origin to be somewhere closeby. Typically, we set the origin to be the location of the first waypoint. Taking this into account, the new conversions are:
\[x = radEarth * \pi /180 * \cos(latOffset) * (longitude - longOffset)\] \[y = radEarth * \pi /180 * (latitude - latOffset)\]
where latOffset and longOffset are the latitude and longitude of our new origin.